Question

5-ое задание. Задание очень сложное, нестандартное, советую подумать хорошо.

Answer 1

Фотография справа-налево получилась.

Вобщем, решением 2 нер-ва является круг без границы с центром в точке (2;1) и Rадиусом = sqrt(2) . (x^2 + y^2 -4x - 2y +4 + 1 -4 -1 < -3 ==> (x-2)^2 + (y-1)^2 < 2 ).

Первое нер-во расписываем в систему:

{y>lx-3l , x>=2
{y>l1-xl , x<2

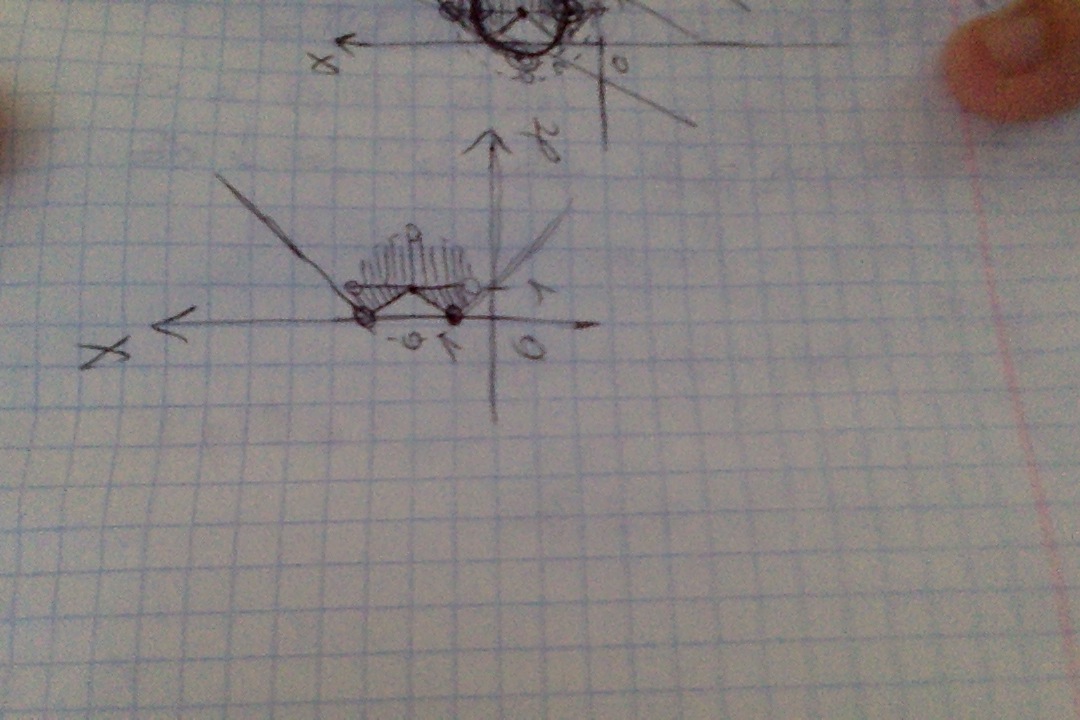
В итоге, строим график кусочно заданной функции модулей и круг без границы, все точки, находящиеся выше ломанной (графика функции - системы модулей), попадающие во внутрь круга являются решениями системы неравенств.

Площадь состоит из полукруга (то что он без границы нам не важно, погрешность при вычислении площади - бесконечно мала) и 2ух секторов по 45 град каждый (опять же, у них отсутствует дуга), это именно сектора, так как радиус нашего круга = sqrt(2). На рисунке нарисовал горизонтальную прямую, чтобы было видно разделение. (На рисунке выколотые точки кажутся, наоборот, включенными, это не так:)  )

По сути, в нашем круге без границы вырезали сектор 90 град. ==> S = 3/4 S круга = 3/4 * pi * r^2 = 1.5 pi

Answer 2

Если честно, то я раньше даже такого понятия не слышал:"круг без границы":)

Answer 3

Если честно, я тоже когда впервые столкнулся с таким геометрическим местом, находился в ступоре - как же это назвать, то)

Answer 4

Даже поправили:) Спасибо

Answer 5

Преобразуем второе неравенство 
$x^2+y^2<4x+2y-3\ x^2-4x+y^2-2y+3<0\ (x-2)^2+(y-1)^2<2$ 
Это уравнение окружности, с центром $O(2;1) R=sqrt{2}$ 
Первое представляет собой прямую  
найдем производную 
$f'(x)=frac{(x-2)(|x-2|-1)}{|x-2|||x-2|-1|}$
Критические точки равны, приравняв  производную к 0 $x=1;2;3$ 
Откуда функция возрастает на 
$xin[1;2]cup[3;infty)$
Функция убывает на 
$xin(-infty;1]cup[2;3]$  
Функция пересекает абсциссу в точке 
$||x-2|-1|=0\ x=1;\ x=3$ 
Следовательно график расположен выше этого графика не  включительно . 
 
Заметим что круг и первое уравнение пересекаются в точках $(1;0)cup(3;0)$ Если решить систему. 
 $||x-2|-1|=y\ x^2+y^2=4x+2y-3$ . 
Теперь найдем площадь как обычно между фигурами  первого неравенства и второго уравнения , затем отнимем от площади круга  
Получим равнобедренный треугольник со сторонами $a=b=1\ c=sqrt{2}\ S_{abc}=frac{2*1}{2}=1$ 
И площадь сегмента   по формуле 
$S=R^2arccos(frac{R-h}{R})-(R-h)sqrt{2Rh-h^2}\ R=sqrt{2}\ h=sqrt{2}-1\ S=2arccos(frac{1}{sqr{2}})-1=2*frac{pi}{4}-1=frac{pi}{2}-1$

Ответ $2pi-frac{pi}{2}+1-1=frac{3pi}{2}$

Answer 6

забыл вычесть площадь треугольника

Answer 7

Даже не знаю, кому лучший отдать:)