Question

Площадь осевого сечения конуса равна 0,6 см2.
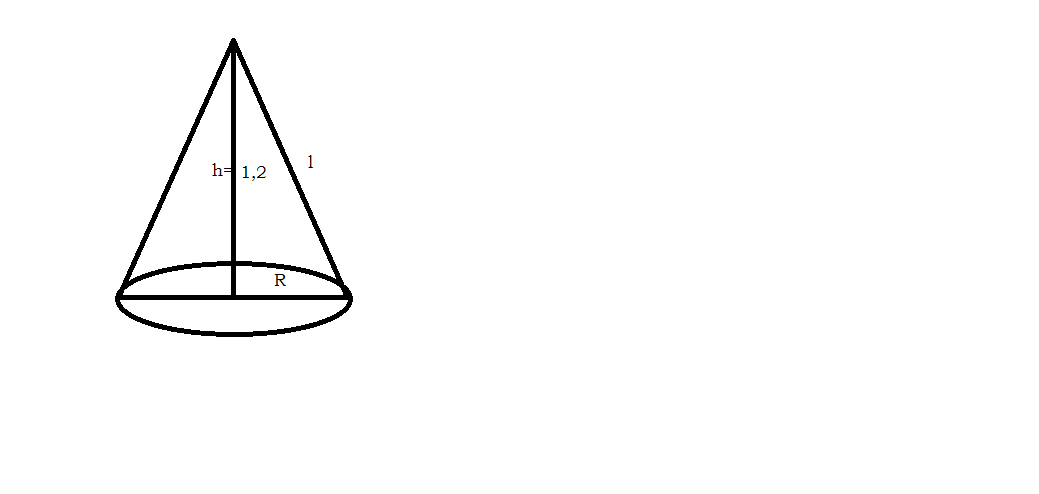
Высота конуса равна 1,2 см.
Вычислите площадь полной поверхности конуса.

Answer 1

Определяем диаметр основания:

S(ос.) = d*h/2, отсюда d

d = 2*S(ос)/h=2*0.6/1.2 = 1 (см),

Радиус основания равна половине диаметру

r = d/2 = 1/2 = 0.5 (см).

Определяем образующую конуса, по т. Пифагора

l² = r² + h²

l=√(r²+h²) = √((0.5)²+(1.2)²) = √1.69 = 1.3 (см)

Определяем площадь полной поверхности конуса

S(пол) = π*r*(r+l) = π *0.5*(0.5+1.3) = 0.5π*1.8=0.9π (см²).

Ответ: 0.9π (см²).

Answer 2

S полн=πR²+πRl, где R - радиус вращения конуса, l - образующая конуса
Осевое сечение конуса - равнобедренный треугольник, площадь которого:
S Δ = a*h/2
а=2S/h
а=2R
2R=2*0,6/1,2
2R=1
R=0,5(см)
Высота конуса делит равнобедренный треугольник на 2 равных прямоугольных треугольника с катетами 0,5см и 1,2см. Образующая конуса (l)- гипотенуза.
По теореме Пифагора:
l=√0,5²+1,2²=1,3(см)
Sполн=πR²+πRl
S полн=0,5²π+0,5π*1,3=0,25π+0,65π=0,9π(см²)≈2,826(см²)