Ответы
Ответ дал:
0
Находим первую производную:

Приравняем производную к нулю, чтобы найти критические точки:





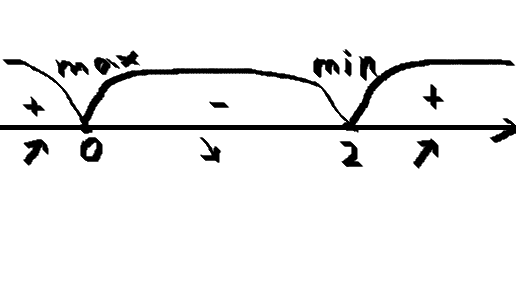
Числовую прямую смотри в вложении:


Ответ:

Приравняем производную к нулю, чтобы найти критические точки:
Числовую прямую смотри в вложении:
Ответ:
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад