Гирька массы m, привязанная к резиновому шнуру, вращается в горизонтальной плоскости с частотой n. Шнур составляет с вертикалью угол альфа. Найти длину нерастянутого шнура Lo, если известно, что для растяжения его до длины L требуется сила F.
Ответы
Ответ дал:
0
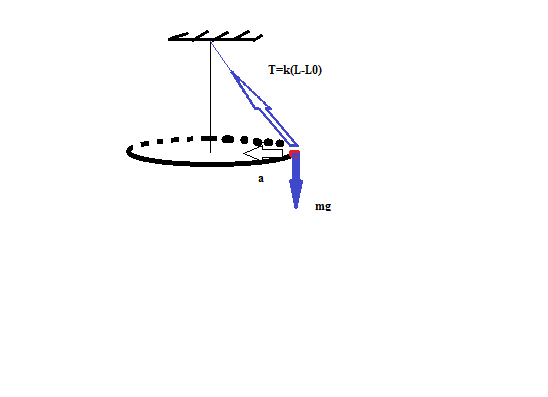
на гирьку, вращающуюся в вертикальной плоскости( конический маятник) действуют силы тяжести, натяжения
в векторном виде

в проекции на ось х

проекция на ось у

где
 изменение длины шнура во время вращения
изменение длины шнура во время вращения



и для того, чтобы найти жесткость
тогда

составляем систему


решаем




теперь делаем подстановку







 Ответ
Ответ
где
ну, и наверное, с точки зрения математики , можно поменять знаки в числителе и знаменателе

Игорь, спасибо за бдительность))
в векторном виде
в проекции на ось х
проекция на ось у
где
и для того, чтобы найти жесткость
тогда
составляем систему
решаем
теперь делаем подстановку
где
ну, и наверное, с точки зрения математики , можно поменять знаки в числителе и знаменателе
Игорь, спасибо за бдительность))
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
11 лет назад