Question

Диагональ трапеции составляет с большим основанием угол в 30градусов, а центр окружности, описанной около трапеции, принадлежит этому основанию. Найдите площадь трапеции, если её боковая сторона равна 2см.(ПОЖАЛУЙСТА РЕШИТЕ С РИСУНКОМ, УМОЛЯЮ)

Answer 1

радиус описанной окружности трапеции R=2
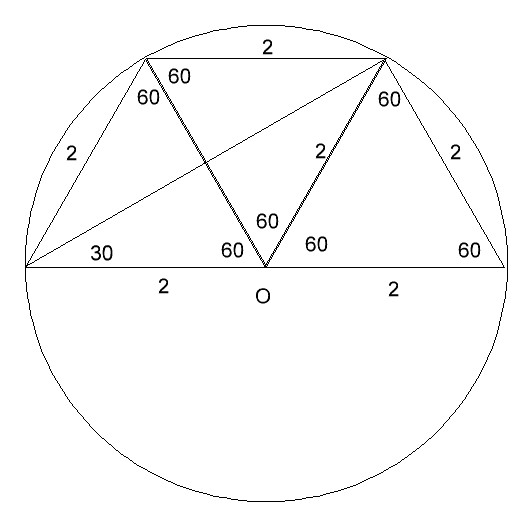
трапеция состоит из 3 равносторонних треугольников со стороной 2
площадь равна 3*2*2*sin(pi/3)/2 = 3*корень(3) = 5,196152

Answer 2

так как центр окружности лежит на нижнем основании, то треугольники образованные нижним основанием, боковой стороной и диагональю - прямоугольные

Answer 3

R = 2 так как боковой треугольник равносторонний

Answer 4

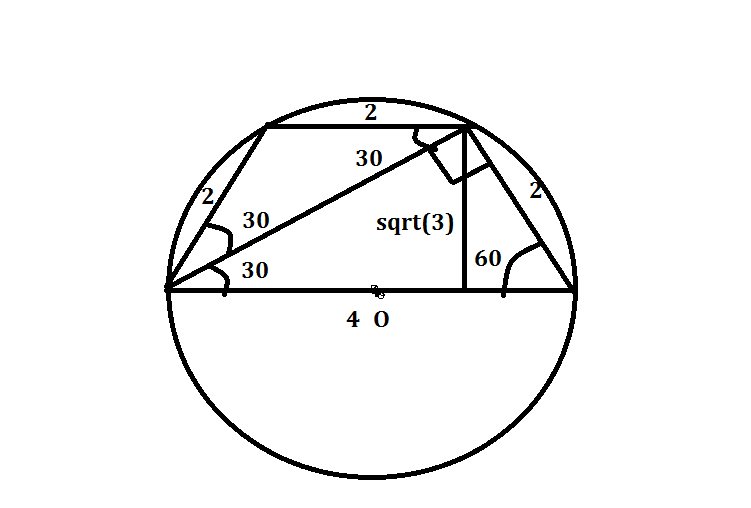
Естественно  тк центр лежит  на основании. То  понятно что основание и есть диаметр. ТО  угол между диагональю  и боковой стороной прямой  .(опирается на диаметр) Трапеция естественно равнобочная.
То  треугольник равнобедренный  ту углы по 30  (внутренние накрест лежащие) Высота:  h=2*sqrt(3)/2=sqrt(3)
Основание: 2/sin30=4
Площадь: s=(2+4)*sqrt(3)/2=3sqrt(3)