Около окружности описана прямоугольная трапеция, боковые стороны которой равны 20 см и 25см. Найдите площадь четырехугольника, вершинами которого являются
точки касания окружности со сторонами трапеции
Ответы
Ответ дал:
0
для описанного 4-угольника суммы противоположных сторон равны)))
20+25 = а+а+15
а = 15 ---меньшее основание трапеции
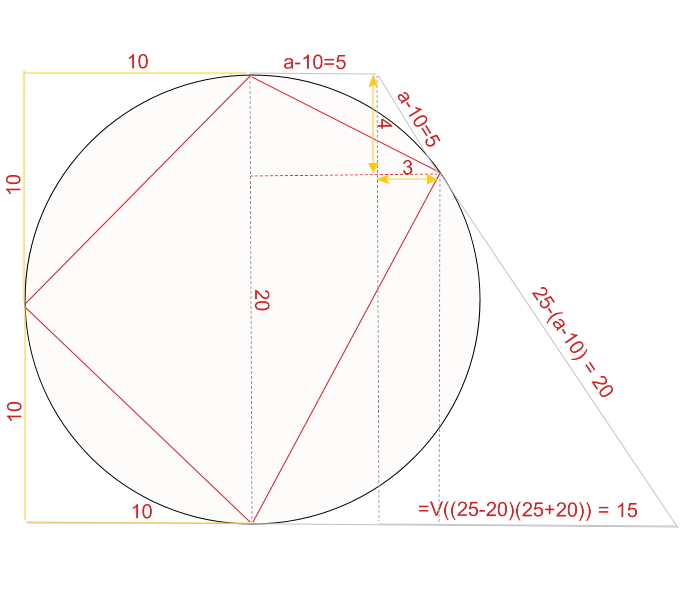
искомая площадь будет состоять из суммы площадей двух прямоугольных (опирающихся на диаметр окружности) треугольников...
один из этих треугольников будет равнобедренным с катетом, равным
10√2, следовательно, его площадь составит 100
для второго треугольника легко находится высота, проведенная к гипотенузе... она = 8)))
и площадь тогда составит 80
Ответ: 180
20+25 = а+а+15
а = 15 ---меньшее основание трапеции
искомая площадь будет состоять из суммы площадей двух прямоугольных (опирающихся на диаметр окружности) треугольников...
один из этих треугольников будет равнобедренным с катетом, равным
10√2, следовательно, его площадь составит 100
для второго треугольника легко находится высота, проведенная к гипотенузе... она = 8)))
и площадь тогда составит 80
Ответ: 180
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад