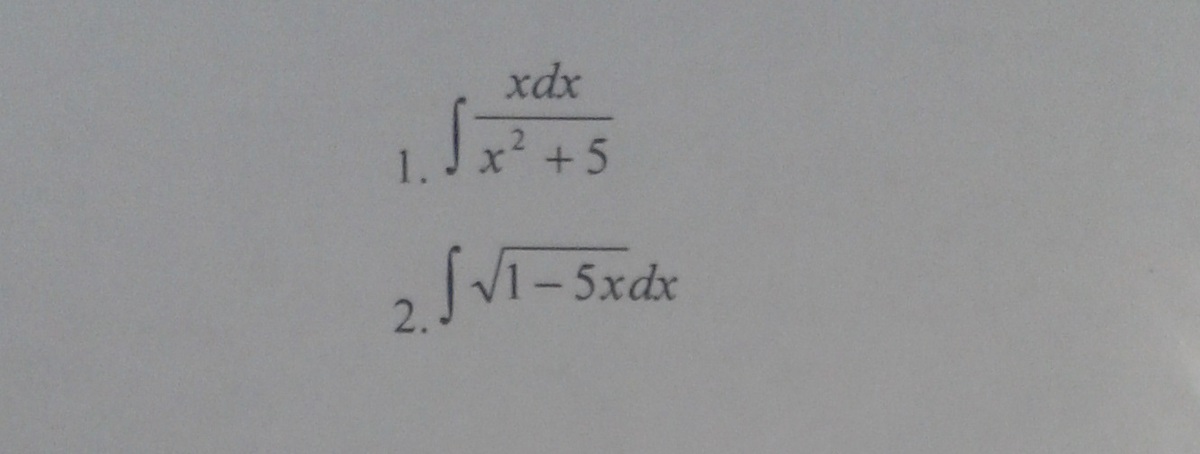Ответы
Ответ дал:
0
Решение
1) Интеграл (1/2)*d(x^2 + 5) / (x^2 + 5) = (1/2)* ln I x^2 + 5 I + C
2) Интеграл (1 - 5x)^(1/2)dx = интеграл (-1/5)*(1 - 5x)^(1/2)d(1 - 5x) =[ (-1/5)*(1-5x)^(1/2 - 1)] / (-1/2) = 2 / 5*(1 -5x)^(1/2)
1) Интеграл (1/2)*d(x^2 + 5) / (x^2 + 5) = (1/2)* ln I x^2 + 5 I + C
2) Интеграл (1 - 5x)^(1/2)dx = интеграл (-1/5)*(1 - 5x)^(1/2)d(1 - 5x) =[ (-1/5)*(1-5x)^(1/2 - 1)] / (-1/2) = 2 / 5*(1 -5x)^(1/2)
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад