Question

объем правильной шестиугольной призмы равен v. определите объем призмы, вершинами которой являются середины сторон оснований данной призмы.

Answer 1

Объем призмы вычисляют произведением площади её основания на высоту. 
V=SH 
Так как данные призмы имеют равную высоту, отношение их объёмов будет отношением площадей их оснований. 
Основание правильной шестиугольной призмы состоит из 6 правильных треугольников.
Поэтому отношение площади основания меньшей призмы к площади основания исходной равно отношению площади одного треугольника меньшего основания к площади одного треугольника большего основания. 
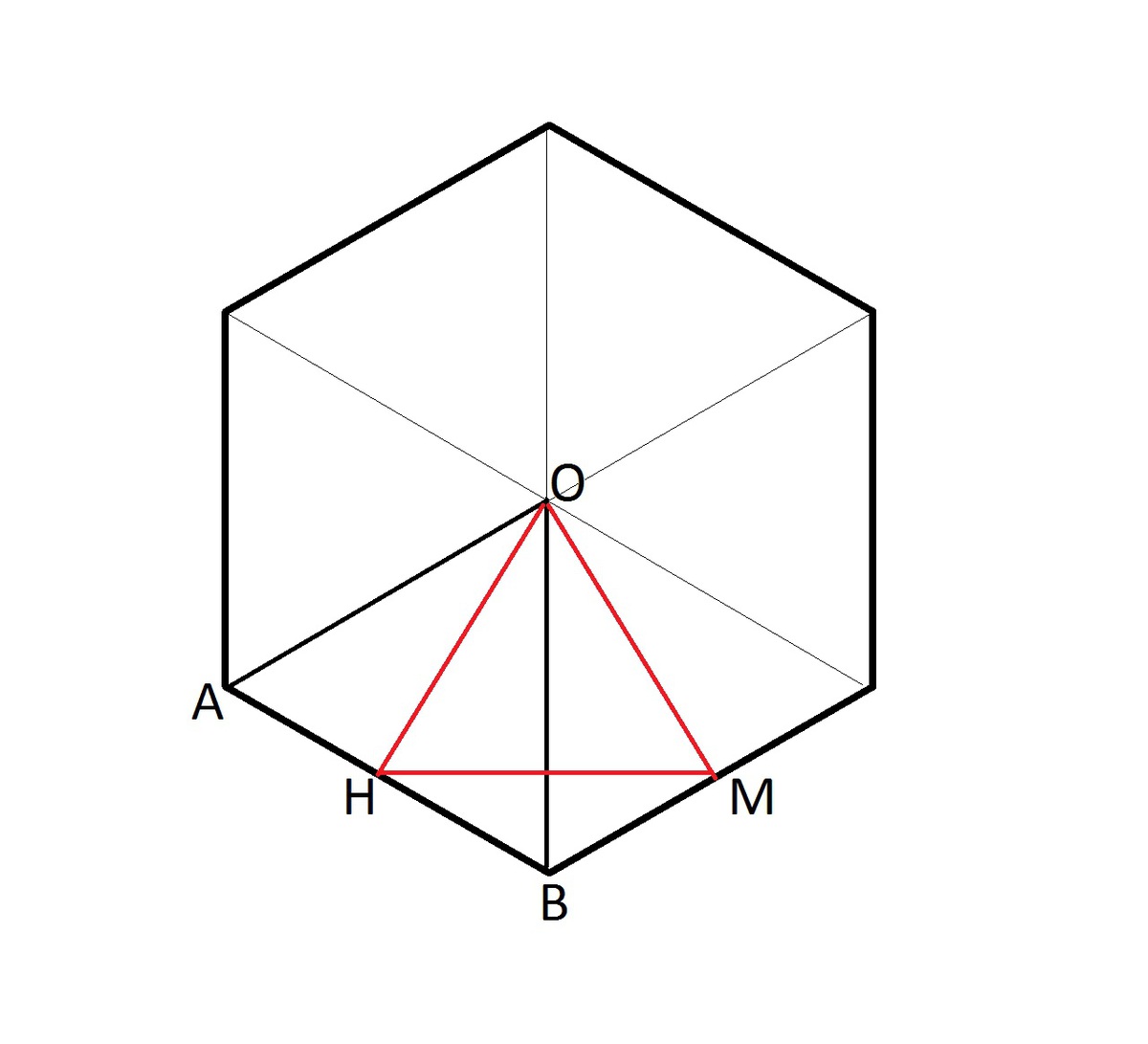
Рассмотрим приложенный рисунок основания призмы. 
Сторона ОН меньшего  основания является высотой треугольника АОВ.
Из 6 таких треугольников состоит большее основание. 
Пусть сторона АО=а. 
Тогда ОН=а*sin(60°)=а√3):2 
Коэффициент подобия треугольников НОМ и АОВ= 
НО:АО=(а√3):2):а=(√3):2 
Отношение площадей подобных фигур равно квадрату коэффициента их подобия: 
S  НОМ: S АОВ=[(√3):2)]²=3/4 
Следовательно, искомый объём равен 3/4 от V, т.е. 3V/4