Помогите:
На рисунке 109 АВ=ВС,AD=DE,угол С=70°,угол EAC=35°.Докажите что DE||AC.
Вот рисунок
Приложения:
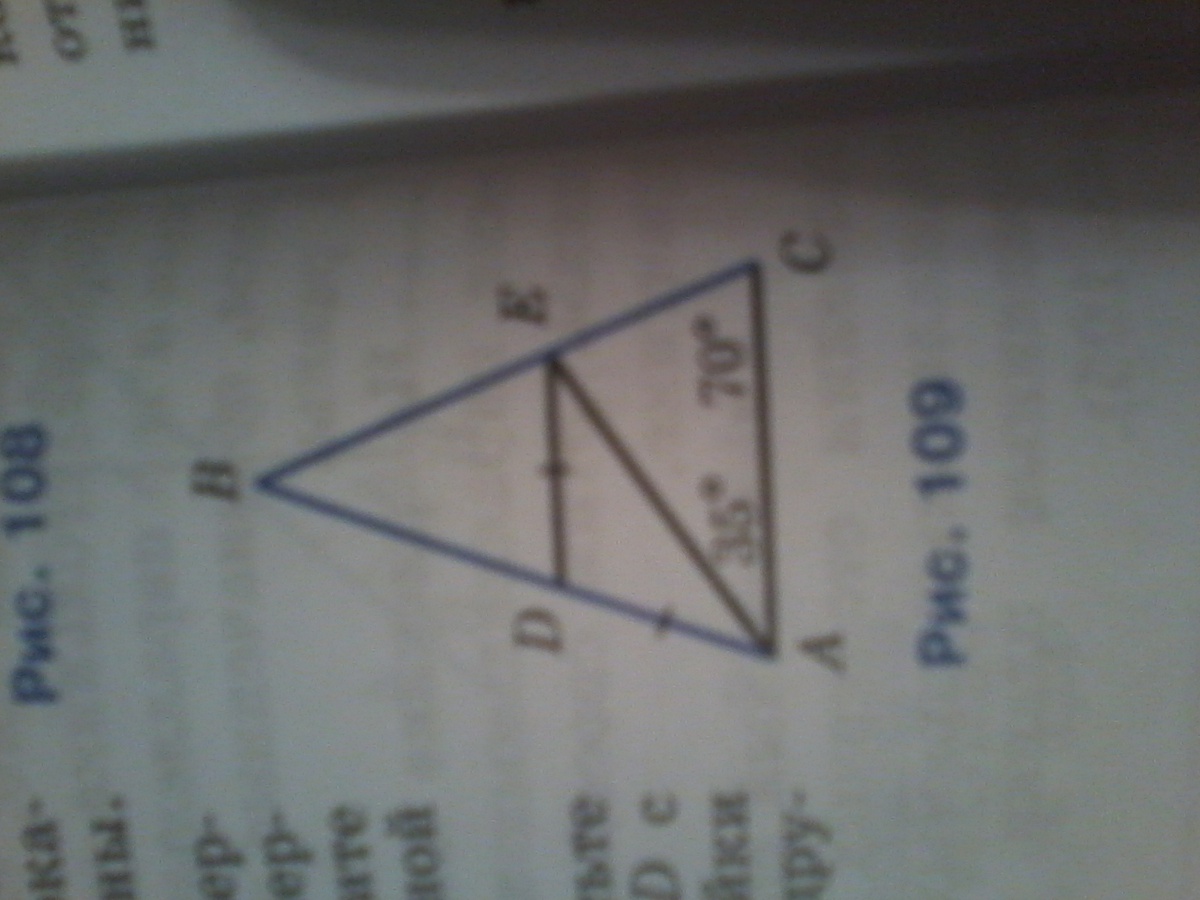
Ответы
Ответ дал:
0
Треугольник АВС равнобедренный, значит <А=<C=70°, как углы при основании.
<EAC=35° (дано). Следовательно, <EAD=<A - <EAC =70°-35°=35°.
Треугольник DEA равнобедренный, так как AD=DE (дано) и
<DEA=<EAD=35° (углы при основании).
Итак, <DEA=<EAC=35°, а это накрест лежащие углы при прямых DE и АС и секущей АЕ. Следовательно, прямые DE и АС параллельны (по признаку параллельности), что и требовалось доказать.
<EAC=35° (дано). Следовательно, <EAD=<A - <EAC =70°-35°=35°.
Треугольник DEA равнобедренный, так как AD=DE (дано) и
<DEA=<EAD=35° (углы при основании).
Итак, <DEA=<EAC=35°, а это накрест лежащие углы при прямых DE и АС и секущей АЕ. Следовательно, прямые DE и АС параллельны (по признаку параллельности), что и требовалось доказать.
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад