Question

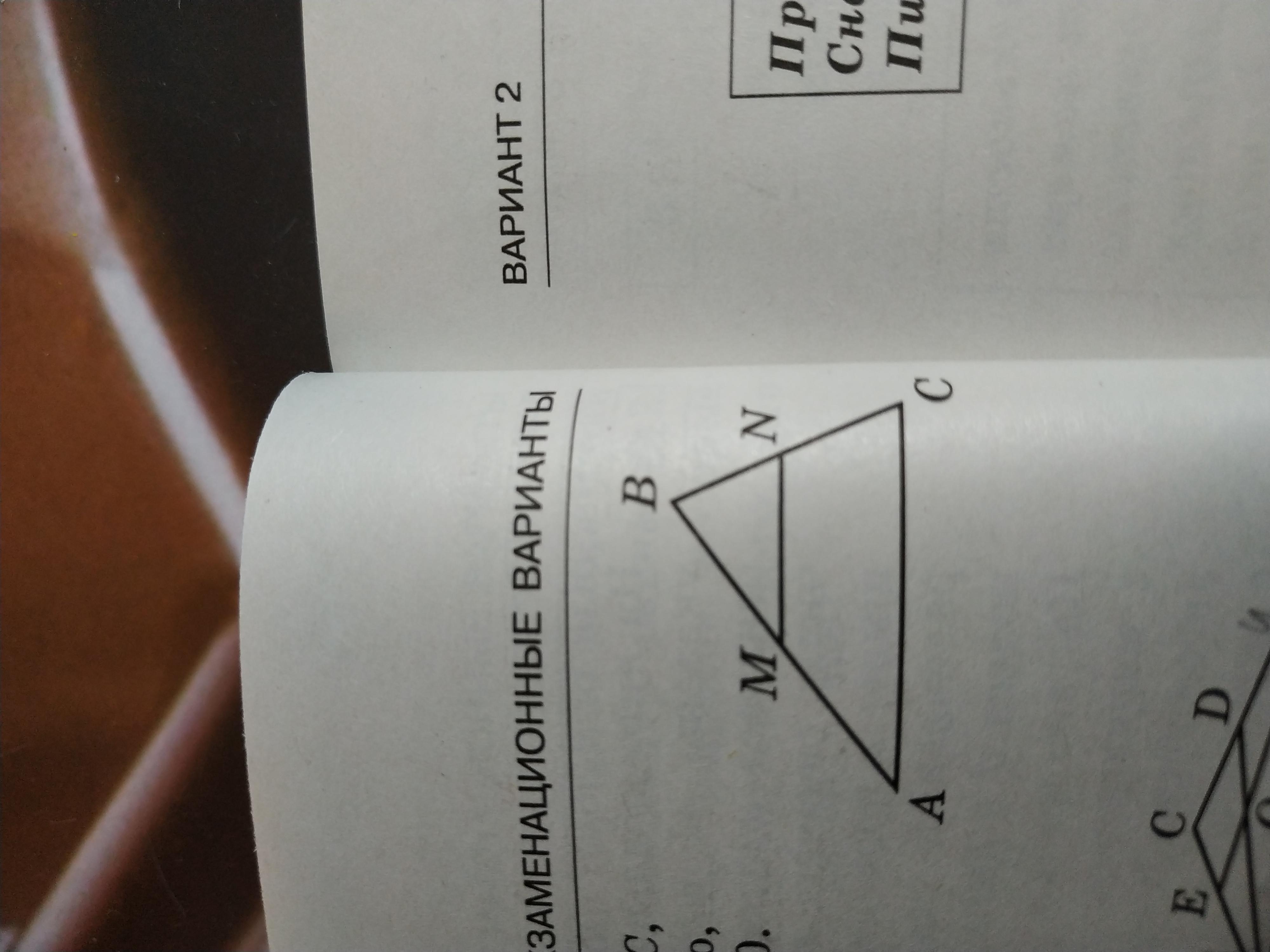
Параллельная стороне AD c треугольника ABC, пересекает стороны AB и BC в точках m и n соответственно, AC равно 20 MN равно 12 .
площадь треугольника ABC равна 50 найдите площадь треугольника mbn
Прошу помогите, сколько решений перепробовала - бесполезно.

Answer 1

Ответ:

0,125 ед.²

Пошаговое объяснение: Рассмотрим треугольники ВМN и ВСА.   В них угол В общий, ∠ВNМ=∠ВСA , как соответственные при МТ ║ АС и секущей ВС, поэтому эти треугольники подобны, а площади подобных треугольников относятся как квадраты их     соответствующих линейных размеров. Т.е. площадь треугольника ВМN так относится к площади треугольника  ВСА, как

(МN/AC)², но это отношение равно (1/20)²=1/400.  Значит, площадь ΔМВN равна 50/400 =0,125/единиц квадратных/