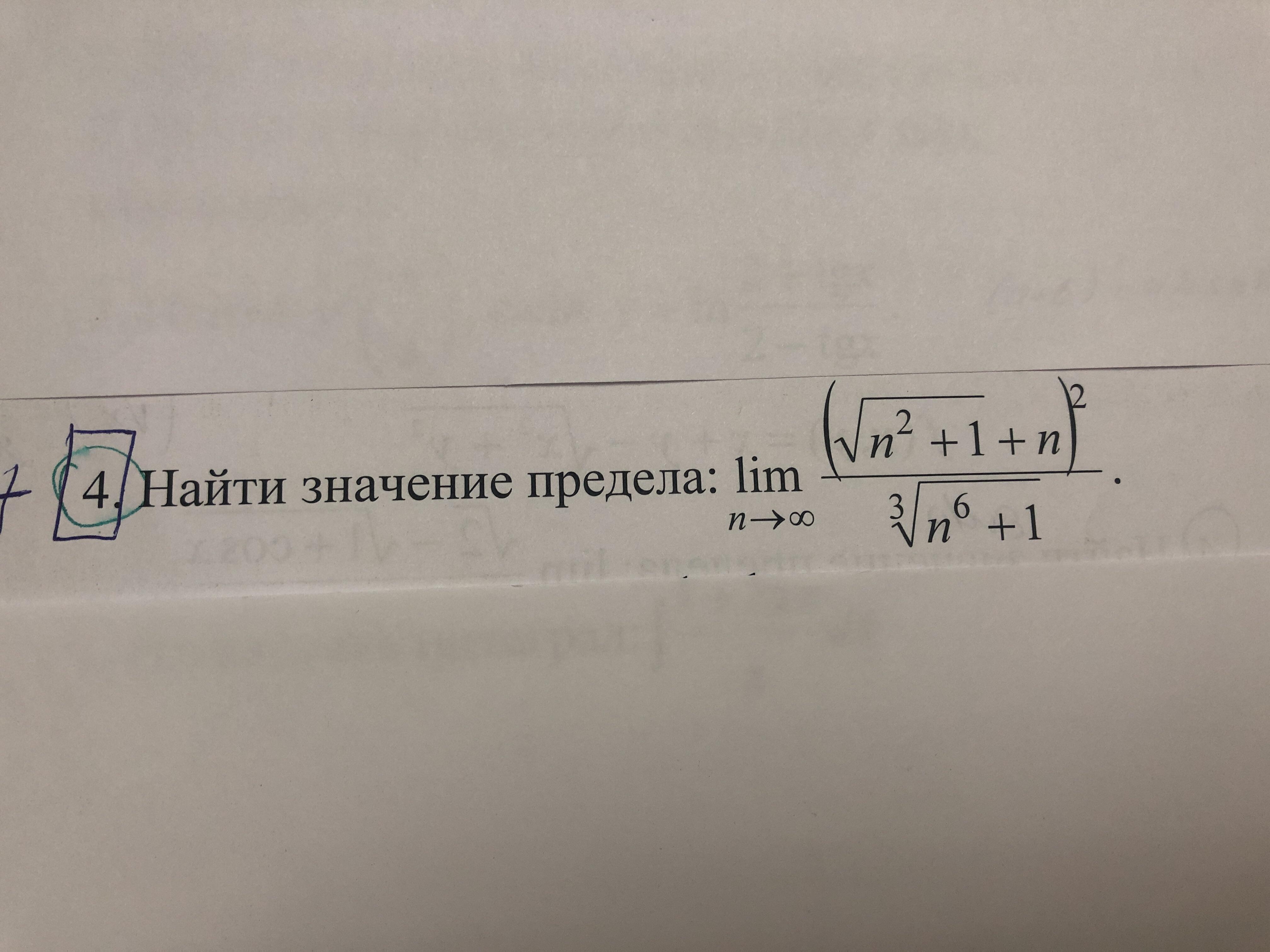Ответы
Ответ дал:
1
фатя98:
У меня ответ 2 получается
и почему же?
2^2 = 4
Если раскрыть числитель по формуле сокращенного умножения (a+b)^2
Зачем? Разделите дробь на 1/n^2 и свойство степени
при раскрытии скобки тоже будет ответ 4
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад