[50б] Производная. Можете расписать формулы или правила , по которым так решилось?
Заранее спасибо)
Приложения:
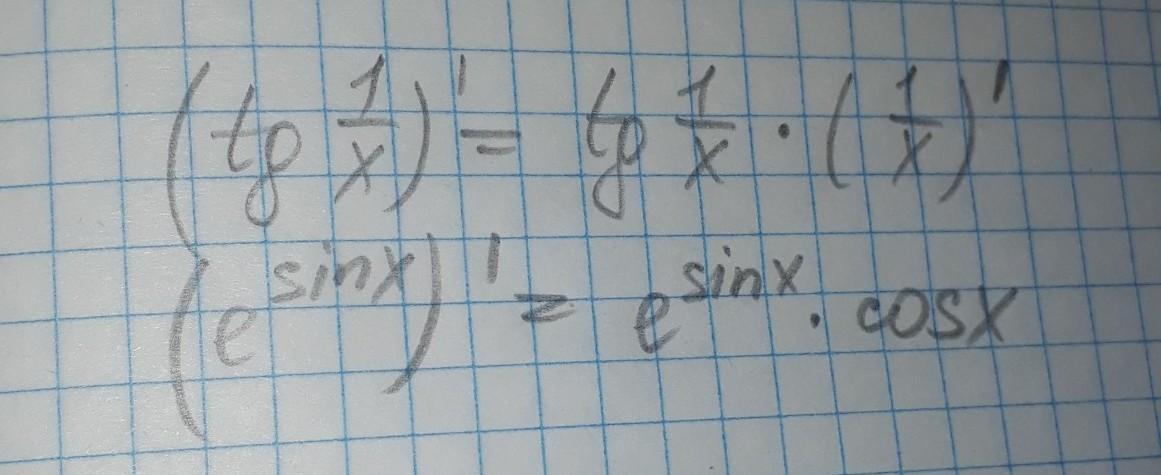
Ответы
Ответ дал:
3
Ответ дал:
3
Это применение правил дифференцирования сложных функций, т.е.
Берем сначала производную от тригонометрической функции, конкретно от тангенса, а потом от его аргумента , т.е. от 1/х, получаете
(-1/х²)*((1/cos²(1/х))
вторая тоже сложная, сначала берете от экспоненты производную, е в степени синус икс, а потом от аргумента , т.е. от синус икс, производная равна косинусу. Окончательно получим е^(sinx)*(cosx)
Кстати, у Вас опечатка в первом примере, Вы забыли поставить штрих возле тангенса. Удачи.
Ryana22222222:
Прошууу помогите с математикой срочно((((
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад