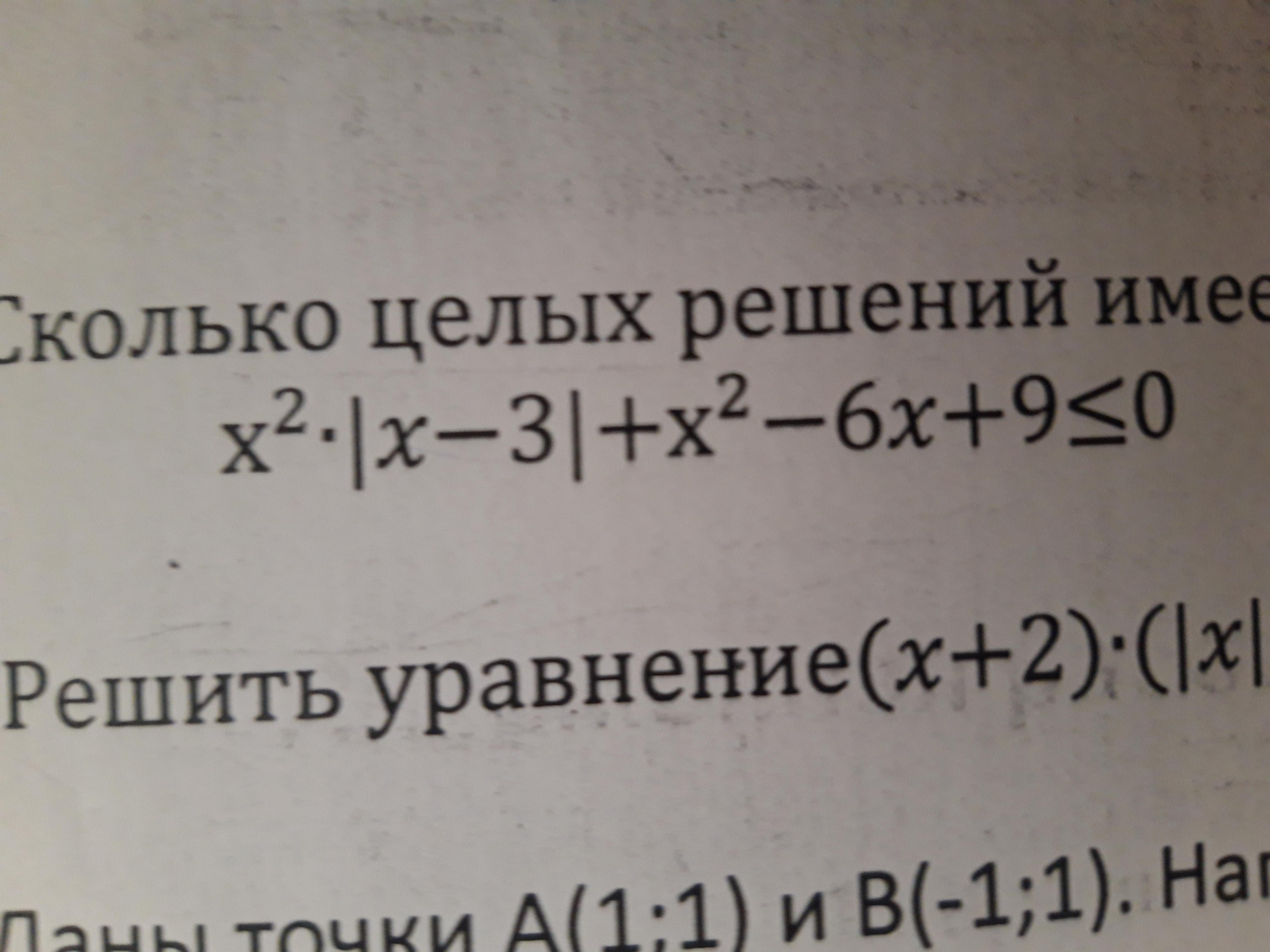Question

Сколько целы решений имеет неравенство

Answer 1

Ответ:

1.

Объяснение:

x²•|x-3|+x²-6x+9 ≤ 0

x²•|x-3|+(x-3)² ≤ 0

x²•|x-3|+lx-3l² ≤ 0

По определению модуля и квадрата

x²•|x-3| ≥ 0 и lx-3l²≥ 0, тогда и вся сумма в левой части неравенства

x²•|x-3|+lx-3l² ≥ 0.

Получили, что неравенство будет иметь решение лишь в том случае, когда

x²•|x-3|+lx-3l² = 0

lx-3l•(x^2 +lx-3l) = 0

lx-3l=0 или x^2+lx-3l=0

1) Первый множитель равен нулю при х=3.

2) Второй множитель мог бы быть равным нулю только в том случае, когда оба неотрицательных слагаемых одновременно были бы нулями при некотором значении х, но х^2= 0 при х=0, а lx-3l = 0 при х =3.

Уравнение корней не имеет.

Неравенство имеет одно целое решение: х = 3.