Решите задачу
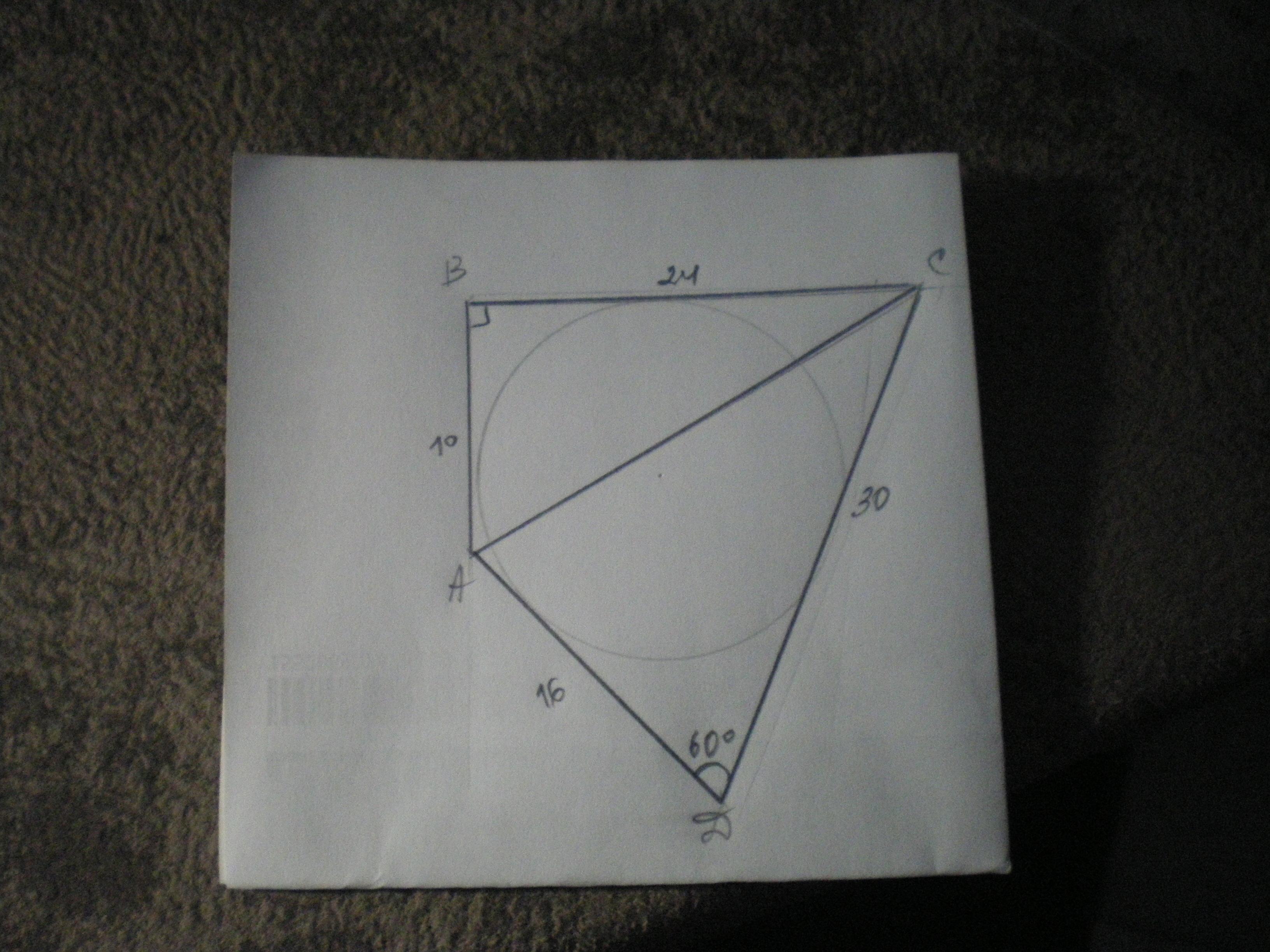
четырёхугольник ABCD описан около окружности, найдите AB и BC, если угол ABC равен 90 градусов, угол ADC равен 60 градусов, AD равно 16 см, CD равно 30 см
cos20093:
Пусть AB = a - 10; поскольку суммы противоположных сторон должны быть равны, BC = a + 10; => (a-10)^2 + (a+10)^2 = AC^2 = 30^2+10^2-30*10; a^2 = 250; это все.
незаметно 10 превратилось в 16 :) чудеса :)
ну, "хитрость" легко можно модифицировать и под "16". Не то, что бы мне было интересно - это тривиальная задачка, но - ради смеха :) Пусть AB = a - 7; поскольку суммы противоположных сторон должны быть равны, BC = a + 7; => (a-7)^2 + (a+7)^2 = AC^2 = 30^2+16^2-30*16 = 676; a^2 = 289; a = 17; AB = 17-7=10; BC = 17+7=24;
Ну, если нужен ответ, откуда взялось "7", то тут можно сказать только одно - магия...
я отвечал сегодня. там стояло условие 16. какие претензии?
а у меня были претензии? Странно... :) наоборот!!!
Ответы
Ответ дал:
21
Ответ:
24 см и 10 см.
Объяснение:
Если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны.
АВ+СD=АD+ВС
Проведем АС; ΔАВС - прямоугольный. Найдем АС из ΔАСD по теореме косинусов:
АС²=СD²+АD²-2*СD*АD*cos 60°=256+900-960*1/2=676;
АС=√676=26 см.
Если АВ+30=ВС+16, то ВС-АВ=14 см;
Пусть ВС=х см, тогда АВ=х-14 см.
По теореме Пифагора АС²=АВ²+ВС²; 676=(х-14)²+х²;
х²+х²-28х+196-676=0
2х²-28х-480=0
х²-14х-240=0
По теореме Виета
х=-10 (не подходит по условию) и х=24.
ВС=24 см; АВ=24-14=10 см.
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
9 лет назад
9 лет назад