Question

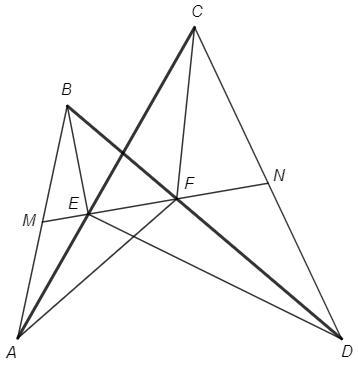
Пусть M - середина стороны AB, а N - середина стороны CD выпуклого четырехугольника ABCD. Прямая MN пересекает диагонали AC и BD соответственно в точках E и F. Доказать, что
AE/EC = BF/FD

Answer 1

Медиана делит площадь треугольника пополам.

S(AFM)=S(BFM)

S(AEM)=S(BEM)

S(AFM)-(AEM) =S(BFM)-S(BEM) => S(EAF)=S(EBF)

Аналогично S(ECF)=S(EDF)  

Площади треугольников с равными высотами относятся как основания.

S(EAF)/S(ECF) =AE/EC

S(EBF)/S(EDF) =BF/FD  

S(EAF)/S(ECF) =S(EBF)/S(EDF) => AE/EC =BF/FD