у равносторонего конуса радиус основания равен

дм. найдите объем конуса (у равнесторонего конуса осевое сечение - правильный треугольник)
Ответы
Ответ дал:
0
Ответ:
2/3π
Пошаговое объяснение:
Так как в осевом сечении получается правильный треугольник, значит боковая сторона конуса равна диаметру.
D=2r=2=боковой стороне конуса
Находим высоту конуса по теореме Пифагора:
h==
Vконуса=1/3 Sосн*h
Sосн=π*r²=2π
Vконуса=1/3*2π*=2/3
π
Ответ дал:
0
Решение на фото/////
Приложения:
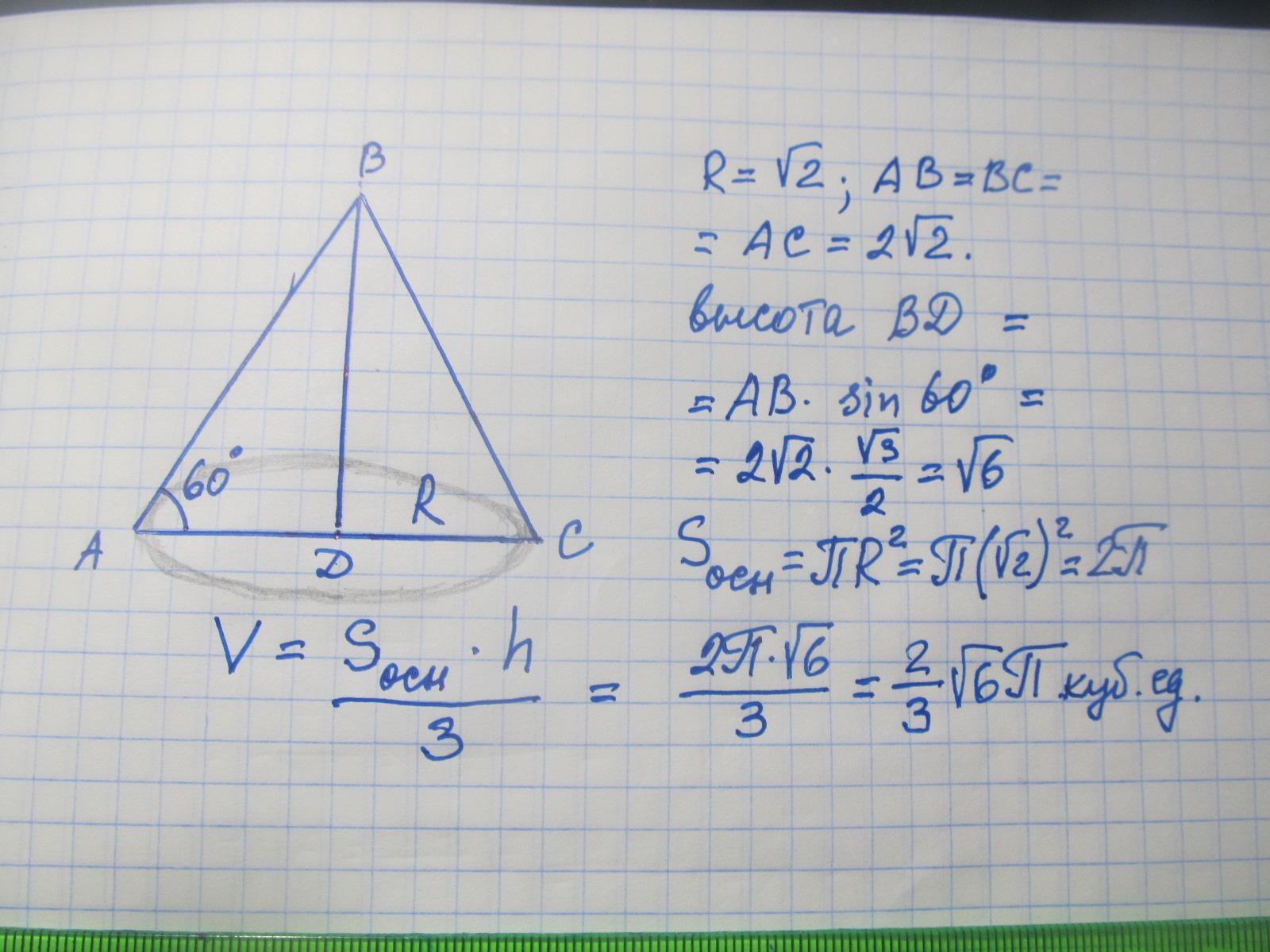
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад