три уравнения по алгебре
Приложения:

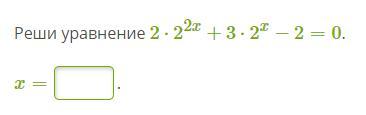
XNyuton:
ответ
х= <_ - 10
второй там 3
3 вариант
незкчто и не вру все правильно если дам ответ мне дадут нарушение
спасибо, а в третьем знаешь что?
Ответы
Ответ дал:
0
Ответ:
Объяснение:
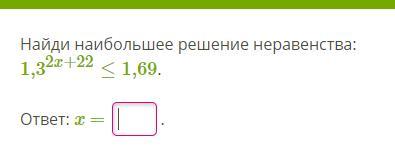
1 . Розв"язки нерівності х ≤ - 10 . В - дь : x = - 10 .
2 . Правильна відповідь : хЄ (- ∞ ; 0,4 ] - 1 - ий варіант відповідей .
3 . 2* 2²ˣ + 3* 2ˣ - 2 = 0 ; введемо нову змінну у = 2ˣ , у > 0 .
2у² + 3y - 2 = 0 ;
D = 25 > 0 ; y₁ = - 2 < 0 ; y₂ = 1/2 .
Повернемося до змінної х :
2ˣ = 1/2 ;
2ˣ = 2⁻¹ ;
х = - 1 . В - дь : x = - 1 .
почему решение выполнено на хохлянском языке?
Ответ дал:
0
Объяснение:
Если a > 1, то f(x) > g(x);
если 0 < a < 1, то f(x) < g(x).
1.
Наибольшее значение неравенства: -10
2.
3.
Выполним замену переменной:
Получим уравнение:
Так как t > 0, то подходит только первый корень.
Сделаем обратную замену:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад