В треугольнике одна из сторон, образующих угол в 120º, больше другой стороны, образующей этот угол на 6 см и на 6 см меньше третьей стороны. Найдите площадь этого треугольника.
Ответы
Ответ дал:
0
Ответ:
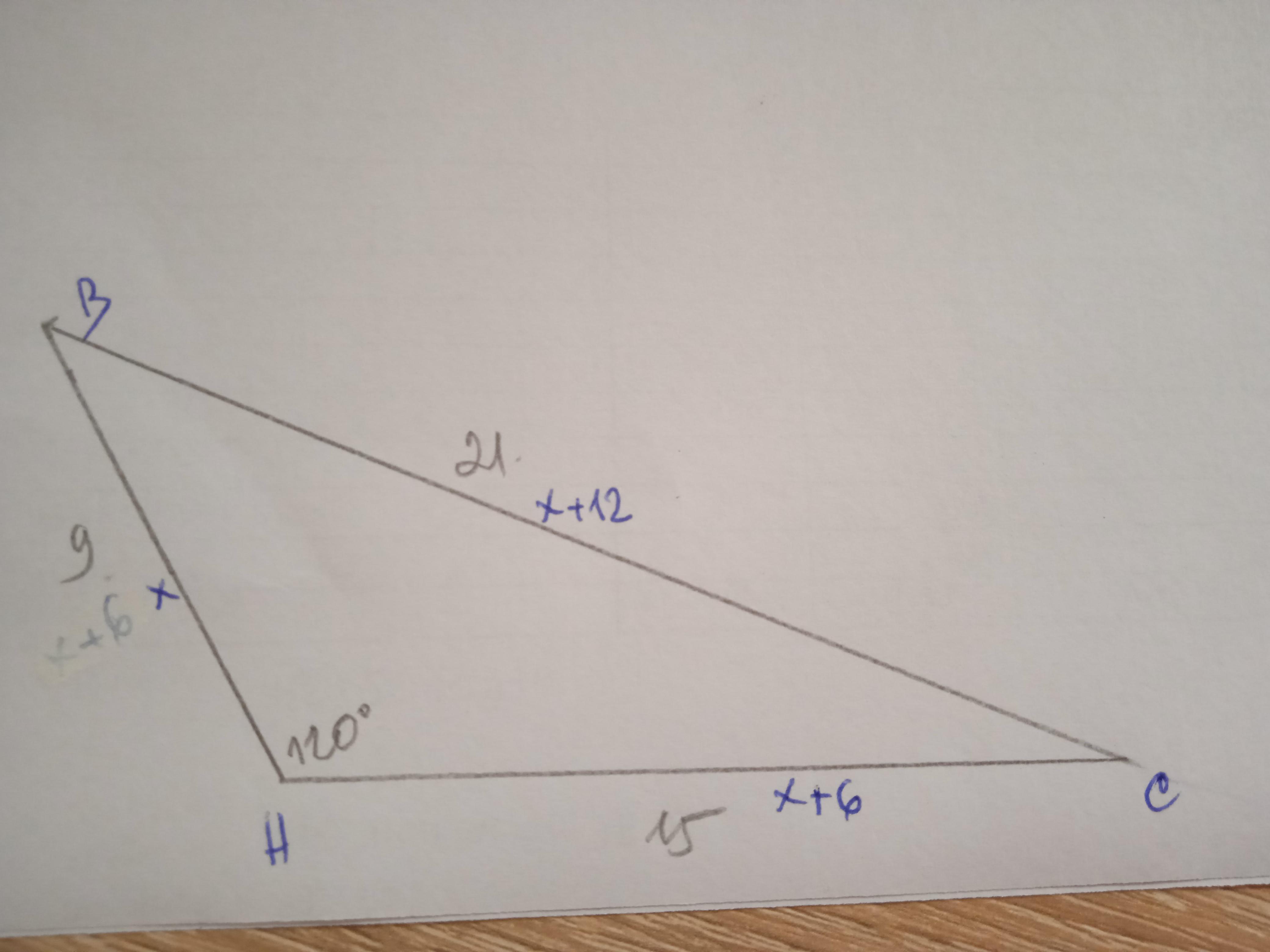
решение смотри на фотографии
Приложения:

Пеппер:
15+6=21 cм
ещё раз спасибо
Ответ дал:
0
Ответ:
67,5√3/2 см²
Объяснение:
Дано: ΔАВС, ∠А=120°, АВ-АС=6 см, ВС-АВ=6 см. S - ?
Пусть АВ=х см, тогда АС=х+6 см, ВС=х+6+6=х+12 см.
По теореме косинусов
ВС²=АВ²+АС²-2*АВ*АС*cos120°
(х+12)²=х²+(х+6)²-2х(х+6)*(-0,5)
х²+24х+144=х²+х²+12х+36-(2х²+12х)*(-0,5)
24х+144=х²+12х+36+х²+6х
х²-3х-54=0
По теореме Виета х=-6 (не подходит) х=9.
АВ=9 см, АС=15 см.
S=1/2 * АВ*АС*sin120°=1/2 * 9 * 15 * √3/2 = 67,5√3/2 см²
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад