Question

Найдите радиус окружности вписанной в прямоугольную трапецию основания которой равен 4см и 6 см

Answer 1

Ответ:

2,4 см

Пошаговое объяснение:

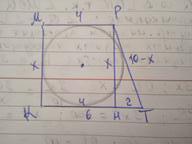
Дано: КМРТ - трапеция, КМ⊥КТ,  МР=4 см,  КТ=6 см.   r - ?

Если в трапецию можно вписать окружность, сумма боковых сторон равна сумме оснований.

Радиус данной окружности равен половине высоты КМ.

КМ+РТ=4+6=10 см.

Проведем высоту РН=КМ=х, тогда РТ=10-х;

КН=МР=4 см,  ТН=6-4=2 см.

ΔТРН - прямоугольный,  по теореме Пифагора

РТ²=РН²+ТН²;  (10-х)²=х²+2²;  100-20х+х²=х²+4;  20х=96;  х=4,8.

r=4,8:2=2,4 см.