Question

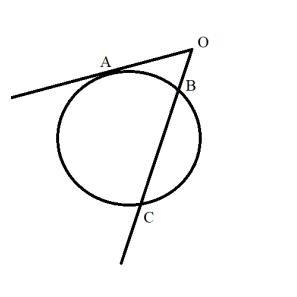
Найдите длину отрезка касательной ОА, если известно, что отрезки OB и BC равны 2 и 6 соответственно.

Answer 1

Ответ:

OA = 4

Объяснение:

Согласно теореме о касательной и секущей: квадрат касательной равен произведению секущей на ее внешнюю часть.
$OA ^{2} = OC * OB$
$OA ^{2} = (OB+BC) * OB$
Подставим числа:
$OA ^{2} = (2+6) * 2$
$OA ^{2} = 16$
Следовательно:
$OA = 4$

Успехов

Answer 2

Ответ:

4 ед.

Объяснение:

Квадрат касательной к окружности равен произведению секущей на ее внешнюю часть.

ОС=2+6=8 ед.

АО²=ОС*ОВ=2*8=16

АО=√16=4 ед.