Вершины треугольника: A(-19,0,0), B(0,19,0) и C(0,0,-6). Найдите расстояние этого треугольника (как плоскости) от точки начала координат.
Ответы
Ответ:
114/√433
Пошаговое объяснение:
Если плоскость проходит через точки М₁(x₁; y₁; z₁), М₂(x₂; y₂; z₂) и М₃(x₃; y₃; z₃), то общее уравнение этой плоскости можно задать как
Раскладываем определитель по первой строке
-114x+114y-361z-2166=0 |:19
-6x+6y-19z-114=0 - общее уравнение плоскости
Расстояние d от плоскости Ax+By+Cz+D=0 до точки M₀(x₀; y₀; z₀) находится по формуле:
Начало координат: M₀(0; 0; 0)
Сначала составляем уравнение плоскости АВС, используя формулу:
x – xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA = 0
Подставим данные и упростим выражение:
x - (-19) y – 0 z - 0
0 - (-19) 19 – 0 0 – 0
0 - (-19) 0 – 0 -6 - 0 = 0
x - (-19) y – 0 z – 0
19 19 0
19 0 -6 = 0
(x – (-19))*(19·(-6)-0·0) – (y - )*(19·(-6)-0·19) + (z – 0)*(19·0-19·1) = 0
(-114)(x - (-19)) + 114(y - ) + (-361)(z - ) = 0
- 114x + 114y - 361z - 2166 = 0 и после сокращения на 19 получаем
6x - 6y + 19z + 114 = 0.
Расстояние в трехмерном пространстве от точки O с координатами (Ox, Oy, Oz) до прямой, заданной уравнением Ax + By + Cz + D = 0, считается так: (см. вкладку).
Начало координат – точка О(0; 0; 0).
Коэффициенты уравнения плоскости: А = 6, В = -6, С = 19, D = 114.
Подставим эти данные в формулу.
d = |6*0 + (-6)*0 + 19*0 + 114|/√(6²+ (-6)²+ 19²) = 114/|/√(36 + 36 + 361) =
= 114/√433 ≈ 5,47849.
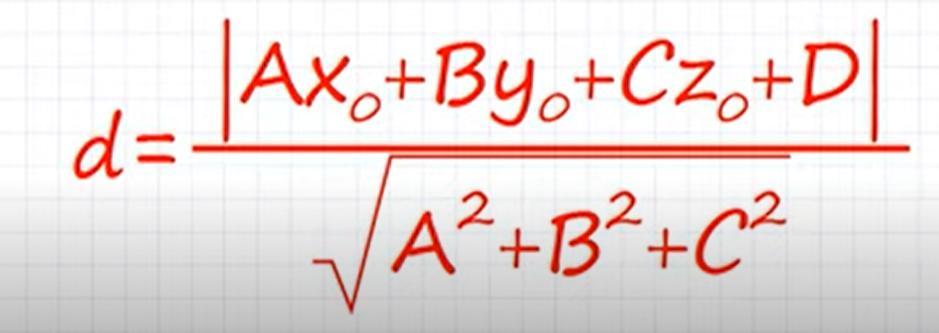
https://znanija.com/task/49882244
https://znanija.com/task/49882220