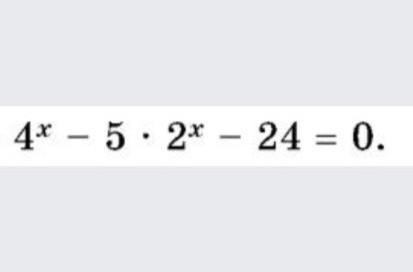Ответы
Ответ дал:
2
Ответ:
x = 3
Объснение:
Сделаем замену:
Решим полученное квадратное уравнение:
Вернемся к замене и подставим вместо t первый корень квадратного уравнения:
Подставим вместо t второй корень квадратного уравнения:
Второй корень не подходит , т.к при возведения положительного числа в степень , полученное значение должно быть больше нуля.
Ответ: x = 3
Ответ дал:
1
Ответ:
решение смотри на фотографии
Приложения:
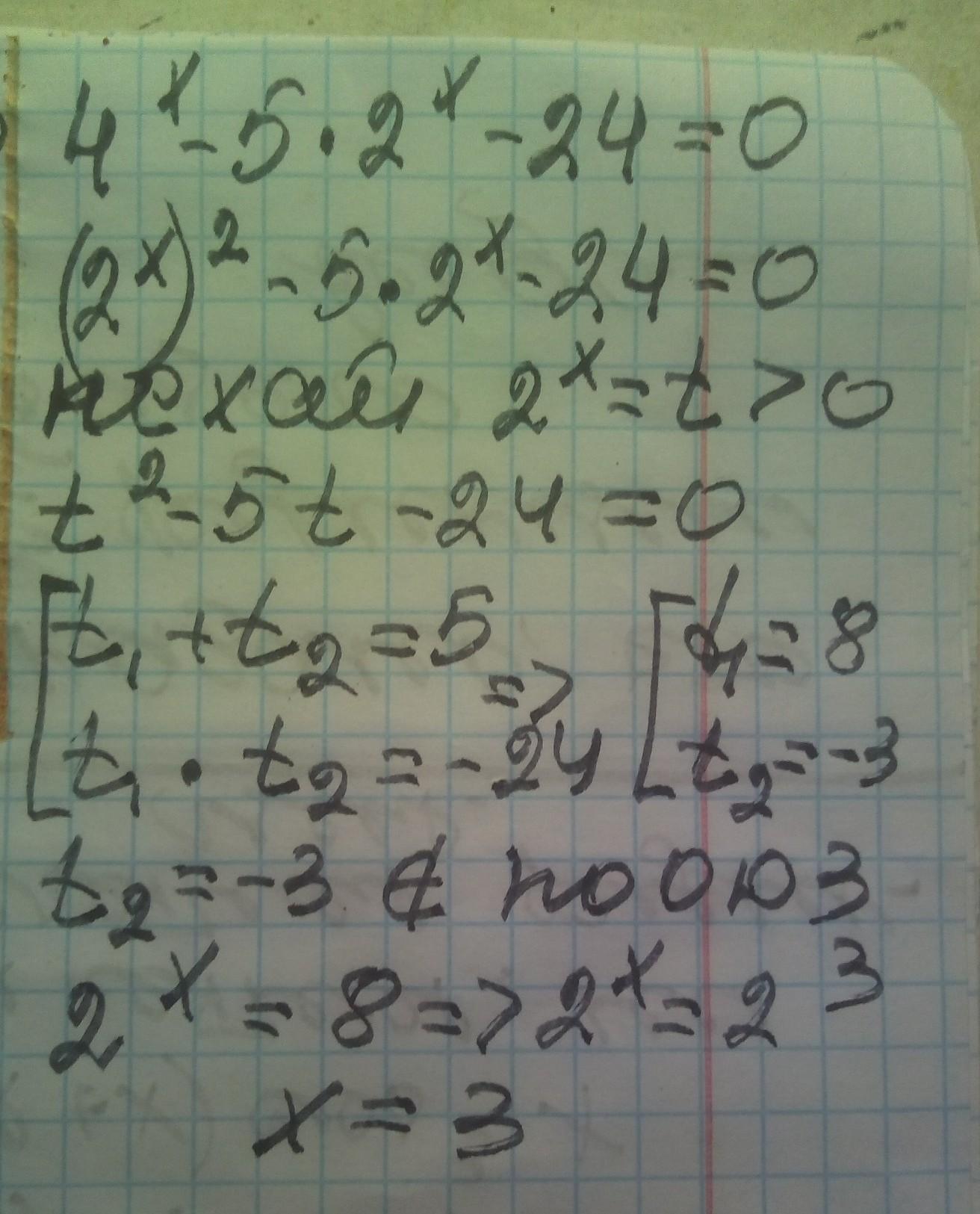
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад