Question

Бісектриса зовнішнього кута при вершині C трикутника ABC перетинає описане коло в точці D. Доведіть, що AD = BD.​

Answer 1

Ответ:

Доказано, что AD = DB.

Объяснение:

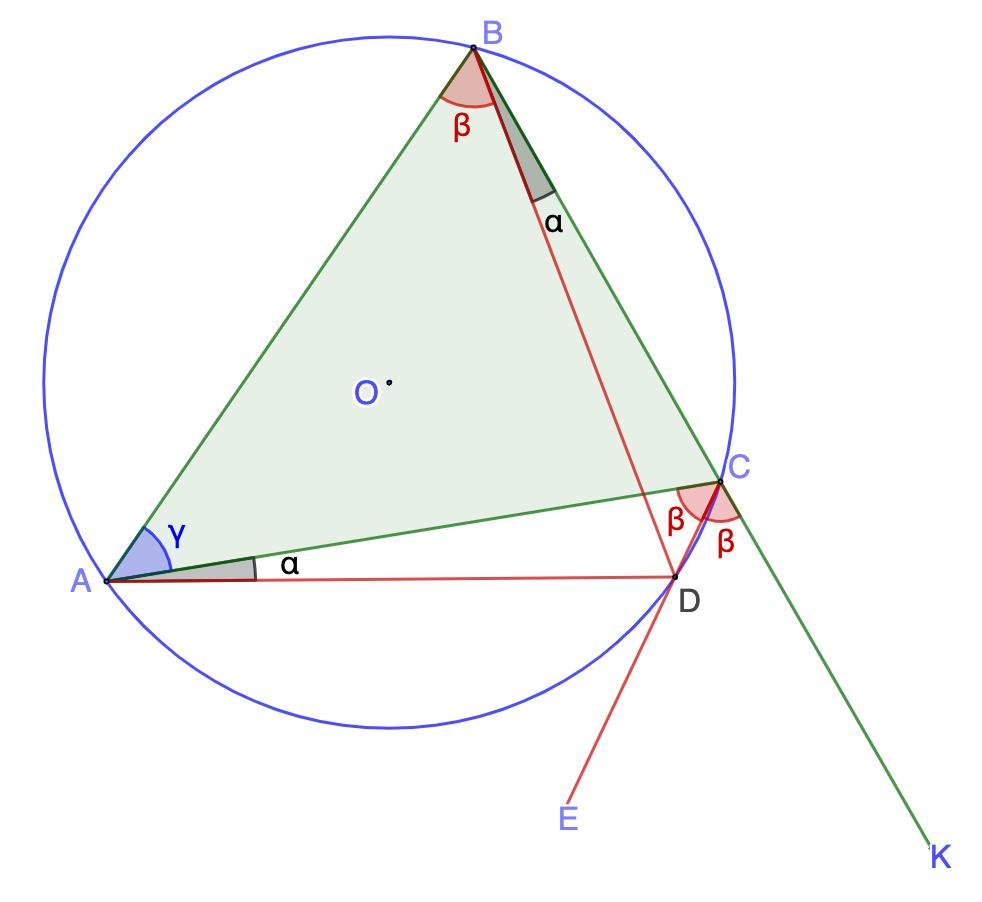
Биссектриса внешнего угла при вершине С треугольника ABC пересекает описанную окружность в точке D. Докажите, что AD = BD.​

Дано: Окр.О;

ΔАВС - вписанный;

∠АСК - внешний; СЕ - биссектриса ∠АСК;

СЕ ∩ Окр.О = D;

Доказать: AD = BD.

Доказательство:

СЕ - биссектриса ∠АСК.

⇒ ∠АСЕ = ∠ЕСК

Пусть ∠АСЕ = ∠ЕСК = β

• Вписанные углы, опирающиеся на одну дугу, равны.

⇒ ∠DBC = ∠CAD (вписанные, опираются на ◡DC)

Пусть ∠DBC = ∠CAD = α

∠ABD = ∠АСD = β (вписанные, опираются на ◡AD)

Пусть ∠ВАС = γ

• Внешний угол треугольника равен сумме углов, не смежных с ним.

⇒ ∠АСК = ∠АВС + ∠ВАС

или 2β = (β + α) + γ   ⇒  γ = 2β - β - α = β - α

Рассмотрим ΔABD.

∠ABD = β;   ∠BAD = γ + α = (β - α) + α = β

• Если в треугольнике два угла равны, то этот треугольник равнобедренный.

⇒ AD = DB.

#SPJ1