В треугольнике ABC угол C равен 90°, CH — высота, AB = 80, синус A = 0,75. Найдите длину отрезка BH.
Ответы
Ответ дал:
0
Ответ:
8
Пошаговое объяснение:
По условию поставленной задачи нам известно, что в треугольнике ABC, угол C равен 90°, CH - высота, AB = 50, sin (A) = 0,4. Для того, чтобы найти длину отрезка BH, выполним следующие действия:
1) Воспользуемся тем, что синус представляет собой отношение противолежащего катета к гипотенузе, а косинус - отношение прилежащего катета к гипотенузе.
Тогда получаем, что sin (A) = cos (B) = BC/AB.
2) Тогда получаем, что ВС = AB * sin (A);
BC = 50 * 0,4 = 20;
3) Рассмотрим треугольник ВНС - прямоугольный (СН - высота).
Значит cos (B) = BH/BC.
4) Тогда получаем, что BH = BC * cos (B);
BH = 20 * 0,4 = 8.
Ответ: 8.
egorovaangelina375:
спасибо большое
стоп,это не та задача
это не правильно
не списуй
ща решу
спасибо большое
проверяй
Ответ дал:
0
решение с рисунком. Конечный результат: сторона НВ = 45
Приложения:
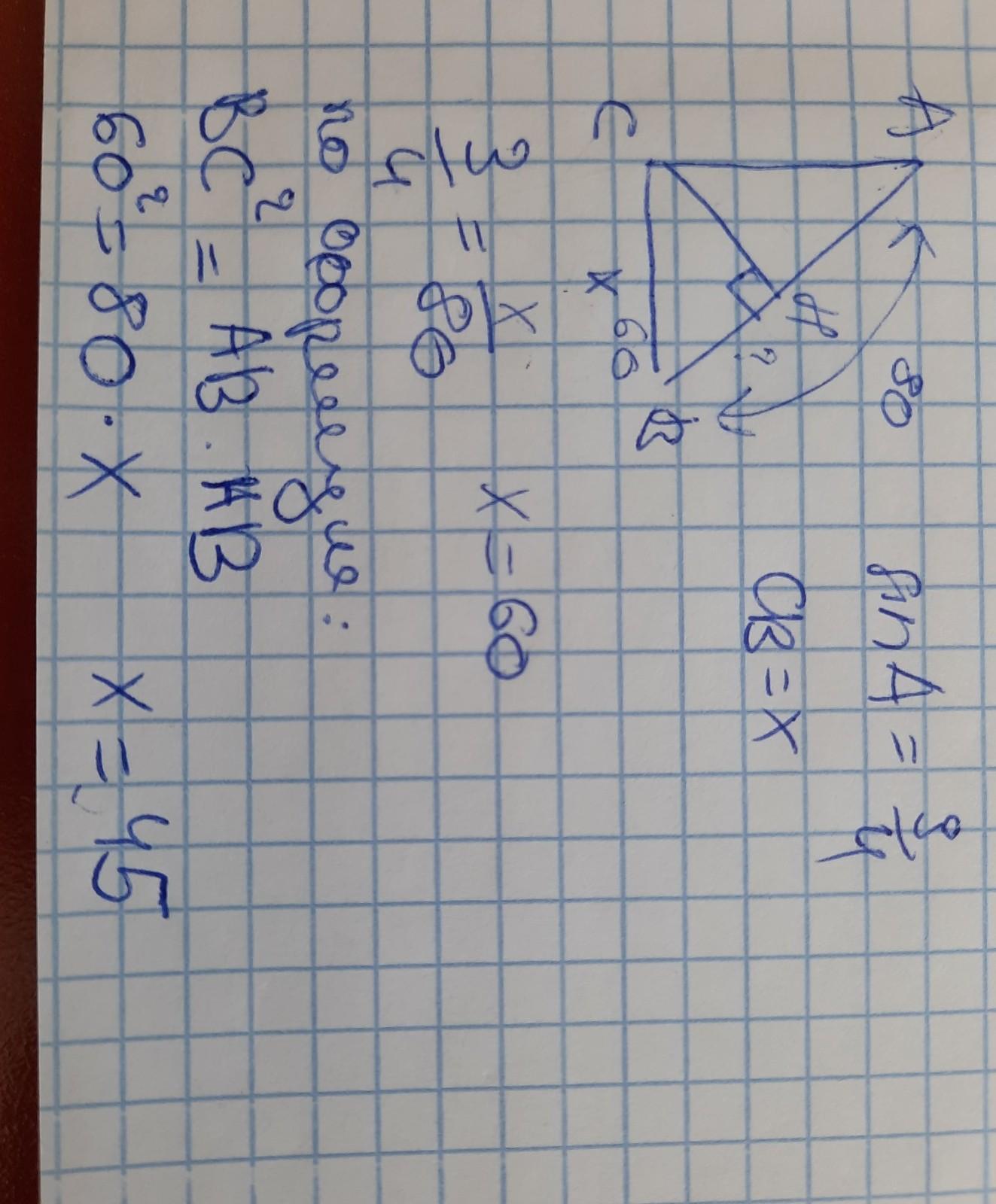
спасибо большое ты мой спаситель
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад