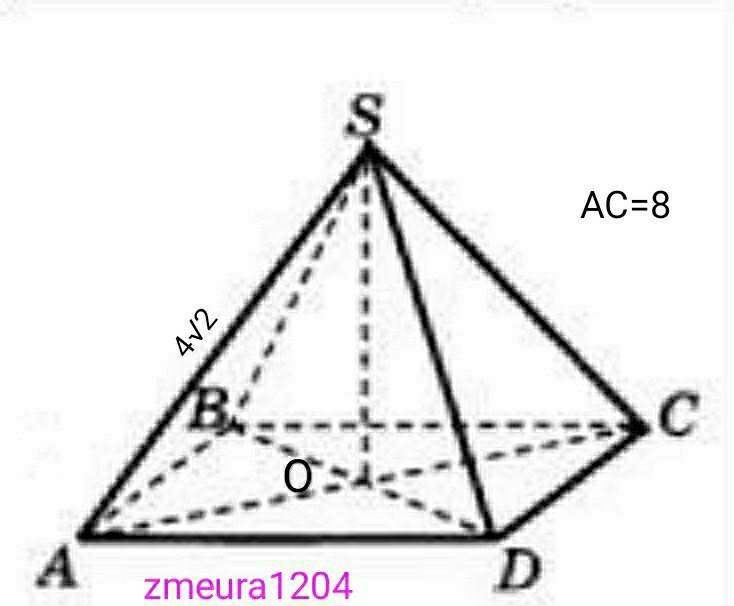
Найти объем правильной четырехугольной пирамиды, у которой боковое ребро равно 4√2 см, а диагональ основания 8 см.
Ответы
Ответ дал:
1
Ответ:
V=128/3 см³
Объяснение:
АО=ОС, свойства квадрата.
АО=АС/2=8/2=4см.
∆АSO- прямоугольный треугольник.
По теореме Пифагора:
SO=√(AS²-AO²)=√((4√2)²-4²)=
=√(32-16)=√16=4см
Sосн=АС²/2=64/2=32см²
V=⅓*Sосн*SO=⅓*32*4=128/3 см³
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад