Question

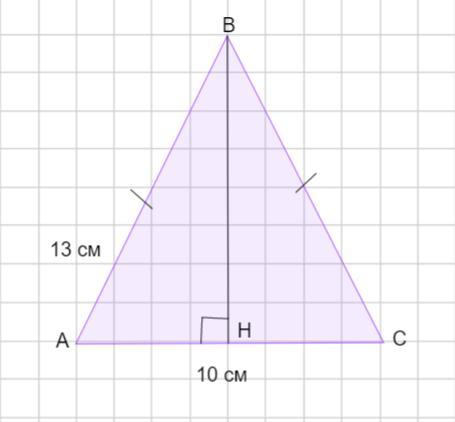
Знайдіть радіуси вписаного та описаного навколо рівнобедреного трикутника кіл, якщо основа трикутника 10 см і бічна сторона 13 см
Допоможіть, з повним розв'язанням

Answer 1

Ответ:

$R =7\dfrac{1}{24}$  см;    $r=3\dfrac{1}{3}$  см.

Объяснение:

Найти радиус вписанной и описанной окружностей около равнобедренного треугольника , если основание треугольника 10 см и боковая сторона 13 см .

Пусть дан Δ АВС - равнобедренный, АВ =ВС = 13 см, АС =10 см.

Проведем высоту ВН . Так как Δ АВС - равнобедренный, то высота, проведенная к основанию является медианой.

Тогда АН =НС = 10: 2 =5 см .

Рассмотрим ΔАНВ - прямоугольный. По теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

АВ ²=АН²+ВН ²;

ВН²=АВ ²-ВН ²;

$BH = \sqrt{13^{2}-5^{2} } =\sqrt{169-25} =\sqrt{144} =12$ см.

Найдем площадь треугольника АВС как полупроизведение стороны на высоту, проведенную к стороне.

$S =\dfrac{1}{2} \cdot AC \cdot BH;\\\\S =\dfrac{1}{2} \cdot 10 \cdot 12=10\cdot 6 =60$ см².

Радиус окружности, описанной около треугольника, найдем по формуле

$R =\dfrac{abc}{4S} ,$  где  a,b,c - стороны треугольника,  S - площадь треугольника .

$R =\dfrac{10\cdot 13\cdot 13}{4\cdot 60} =\dfrac{169}{24}=7\dfrac{1}{24}$  см.

Радиус окружности, вписанной в треугольник , определим по формуле

$r=\dfrac{2S}{P} ,$  где  S - площадь треугольника,  P - его периметр

Р =13+ 13 +10 =36 см.

$r=\dfrac{2\cdot 60 }{36} =\dfrac{2\cdot 10}{6} =\dfrac{10}{3} =3\dfrac{1}{3}$  см.

#SPJ1