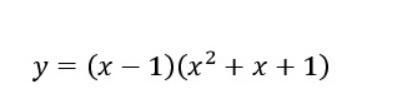Ответы
Ответ дал:
0
Ответ:
3x²
Объяснение:
решение на фото ————
Приложения:
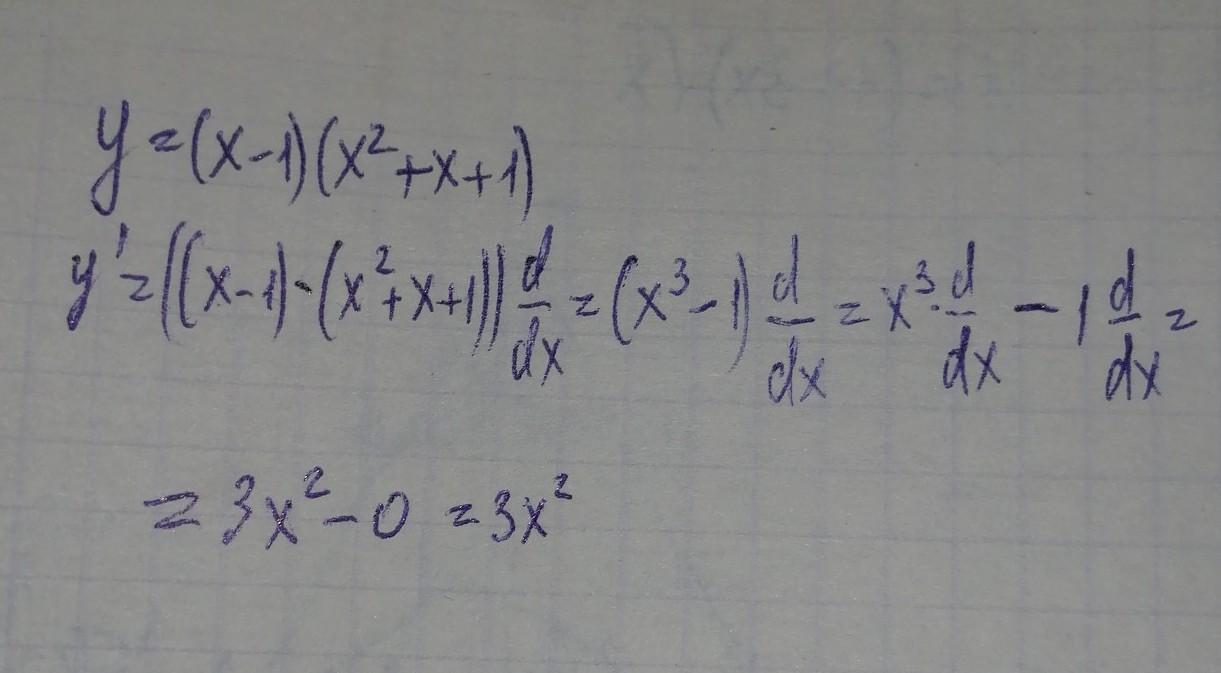
Ответ дал:
0
Ответ:
Производная произведения : .
Или проще преобразовать функцию по формуле разности кубов .
Приложения:

Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад