використовуючи виділення повного квадрату в знаменнику підінтегрального виразу, Срочно
Приложения:
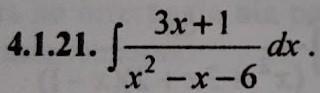
Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
Перевод: Интегрировать используя выделение полного квадрата в знаменателе подынтегрального выражения
Решение. Выделим полный квадрат в знаменателе подынтегрального выражения:
Сделаем замену переменных
Методом неопределенных коэффициентов раскладываем подынтегральную функцию в сумму простых дробей:
Получаем равенство
A·(t+2,5)+B·(t-2,5) = 3·t+2,5 или A·t+2,5·А+B·t-2,5·В = 3·t+2,5.
Приравнивая коэффициенты многочленов получим систему линейных уравнений:
Из системы определим коэффициенты А и В:
Теперь вычислим интеграл
Сделаем обратную замену :
#SPJ1
Вас заинтересует
1 год назад
2 года назад
2 года назад
8 лет назад