Question

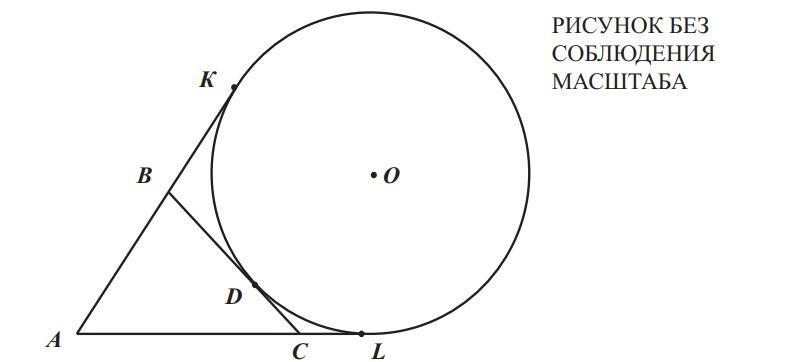
Дана окружность с центром в точке О.
AL, AK и BC – касательные к окружности.
L, D, K – точки касания.
Периметр треугольника АВС равен 13 см.
Найдите длину АК

Answer 1

Ответ:

Длина АК равна 6,5 см.

Объяснение:

Дано: окружность с центром в точке О.

AL, AK и BC – касательные к окружности.

L, D, K – точки касания.

Р(АВС) = 13 см.

Найти: длину АК.

Решение:

• Периметр - сумма длин всех сторон.

Р(АВС)  = АВ + ВС + АС

ВС = BD + DC

⇒ Р(АВС)  = АВ + ВD + DC + АС

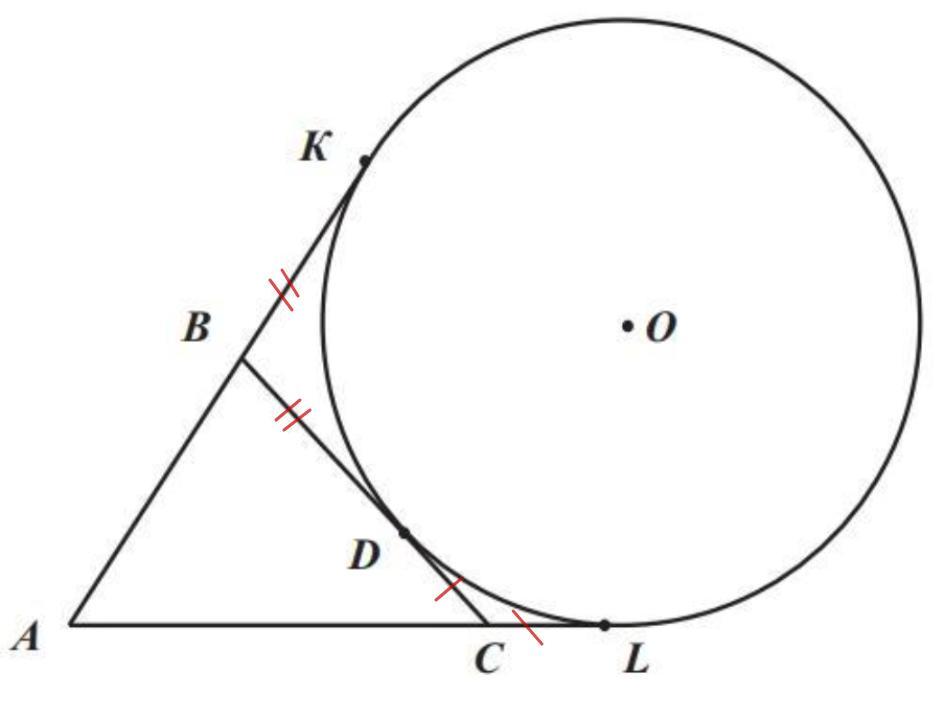
• Отрезки касательных к окружности, проведенных из одной точки, равны.

⇒ BD = BK;   CD = CL

Заменим ВD и DC равными отрезками:

Р(АВС)  = АВ + ВK + CL + АC

АВ + ВK = AK;    CL + АC = AL

⇒ Р(АВС) = AK + AL

13 = AK + AL

AK и AL - касательные

⇒ AK = AL = 13/2 = 6,5 (см)

Длина АК равна 6,5 см

#SPJ1