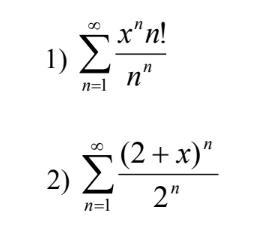Question

Решить оба, всё расписать. Найти область сходимости степенного ряда.

Answer 1

Ответ:

1) (-e;e); 2) (-4;0).

Пошаговое объяснение:

1).  $\sum\limits_{n=1}^{\infty}c_n(x-x_0)^n,$  где $c_n=\dfrac{n!}{n^n},\ x_0=0.$

Найдем радиус сходимости ряда:

 $R=\lim\limits_{n\to \infty}\left|\dfrac{c_n}{c_{n+1}}\right|=\lim\limits_{n\to \infty}\dfrac{n!\cdot (n+1)^{n+1}}{n^n\cdot (n+1)!}=\lim\limits_{n\to \infty} \left(\frac{n+1}{n}\right)^n=\lim\limits_{n\to \infty} \left(1+\dfrac{1}{n}\right)^n=e.$

Интервал сходимости

                                   $(x_0-R;x_0+R)=(-e;e).$

Остается исследовать ряд в точках e и -e.

В точке e имеем ряд

                                            $\sum\limits_{n=1}^{\infty}\dfrac{e^n\cdot n!}{n^n}.$

Найдем предел общего члена этого ряда при n, стремящемся к бесконечности:

$\lim\limits_{n\to \infty}\dfrac{e^n\cdot n!}{n^n}=\lim\limits_{n\to \infty} \dfrac{e^n\cdot \sqrt{2\pi n}\cdot \left(\dfrac{n}{e}\right)^n}{n^n}=\lim\limits_{n\to \infty}\sqrt{2\pi n}=\infty.$

Но по необходимому признаку сходимости, если предел общего члена ряда не равен нулю, ряд расходится.

В точке -e имеем ряд

                                       $\sum\limits_{n=1}^{\infty}\dfrac{(-1)^ne^n\cdot n!}{n^n}.$

По модулю общий член этого ряда совпадает с общим членом ряда в предыдущем случае, поэтому он также стремится к бесконечности. Поэтому и в точке -e степенной ряд расходится. Вывод: область сходимости ряда совпадает с его интервалом сходимости.

2) $c_n=\dfrac{1}{2^n},\ x_0=-2.$

Найдем радиус сходимости:   $R=\lim\limits_{n\to \infty}\left|\dfrac{c_n}{c_{n+1}}\right|=\lim\limits_{n\to \infty} \dfrac{2^{n+1}}{2^n}=2.$

Интервал сходимости $(x_0-R;x_0+R)=(-2-2;-2+2)=(-4;0).$

В точке 0 имеем ряд $\sum\limits_{n=1}^{\infty}\dfrac{2^n}{2^n}=\sum\limits_{n=1}^{\infty}1.$ Общий член не стремится к нулю; ряд расходится.

В точке -4 имеем ряд  $\sum\limits_{n=1}^{\infty}\dfrac{(-1)^n2^n}{2^n}=\sum\limits_{n=1}^{\infty}(-1)^n.$ Общий член не стремится к нулю; ряд расходится. Вывод: область сходимости ряда совпадает с его интервалом сходимости.

Замечание. Мы воспользовались формулой Стирлинга

                                           $n!\sim\sqrt{2\pi n}\cdot \left(\dfrac{n}{e}\right)^n.$