Question

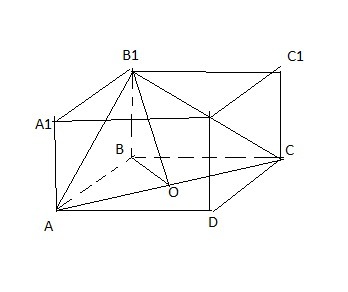
основание правильной четырехугольной призмы служит квадрат, диагональ которого равна d. через диагональ основания и противолежащую вершину верхнего основания проведена плоскость под углом 45 к нему. найдите объём призмы

Answer 1

Т.к. все три точки сечения призмы лежат попарно в одних и тех же плоскостях, то сечение строится попарным соединением точек - получаем в сечении ΔAB1C

Т.к. четырехугольники AA1B1B и BB1C1C равны, то равны и их диагонали AB1 и B1C ⇒ ΔAB1C равнобедренный.

Проведем медиану B1O в ΔAB1C, одновременно она будет и высотой ⇒ B1O ⊥ AC

Проведем медиану BO в равнобедренном ΔABC, одновременно она будет и высотой ⇒ BO ⊥ AC

Значит BOB1  будет углом между плоскостью сечения и нижним основанием, а т.к. нижнее и верхнее основание параллельны, то он равен углу между плоскостью сечения и верхним основанием, т.е. 45°

Из ΔBOB1, зная, что BO равно половине диагонали квадрата, найдем, что высота призмы BB1 = d /2

Из прямоугольного равнобедренного ΔABC  с гипотенузой AC = d, найдем $AB=frac{d}{sqrt{2}}$

Объем призмы найдем как произведение площади основания на высоту:

$V=frac{d}{sqrt{2}}*frac{d}{sqrt{2}}*frac{d}{2}=frac{d^3}{4}$