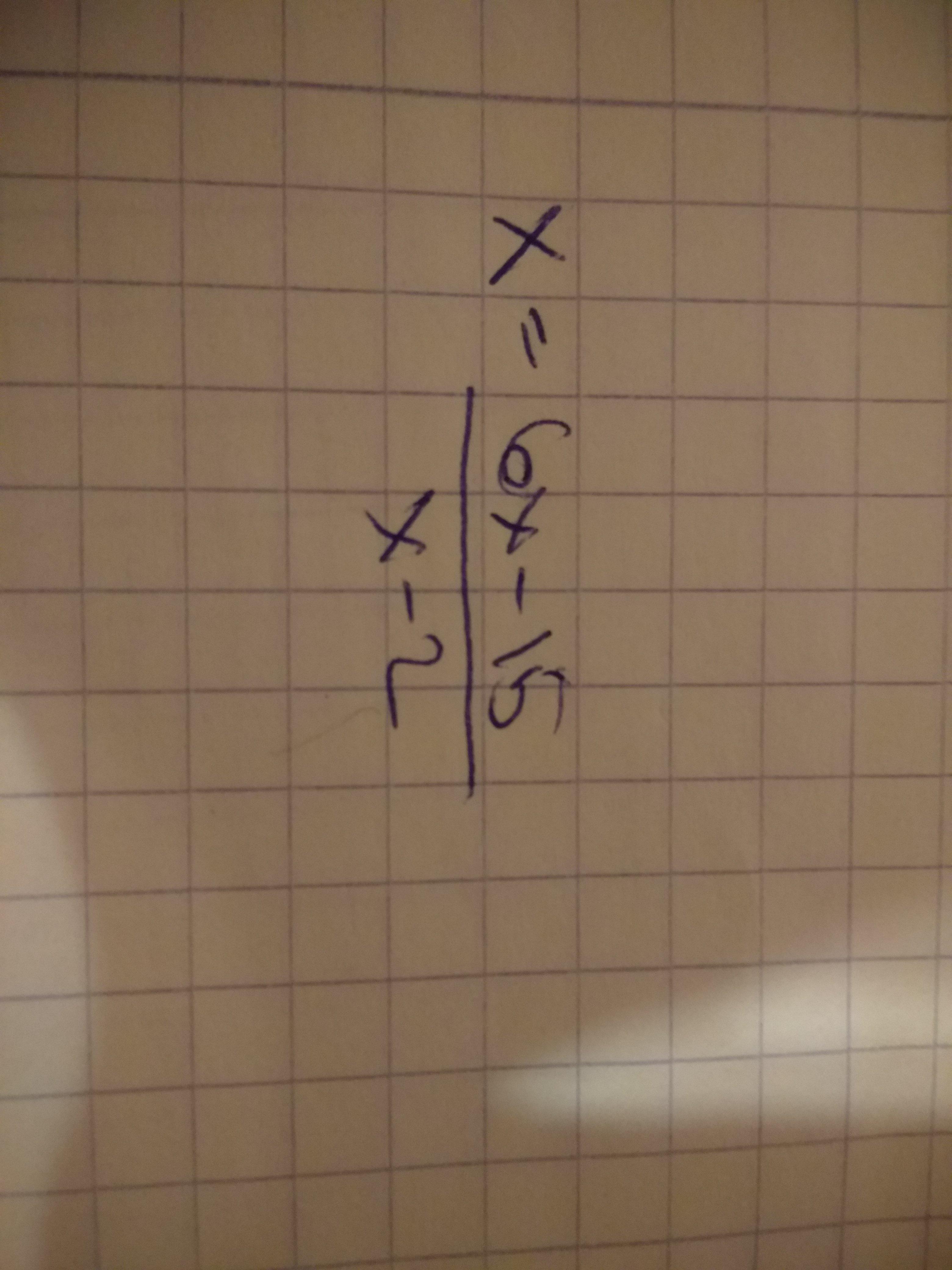Question

Помогите пожалуйста решить, надо найти корень уравнения

Answer 1

$x = frac{6x - 15}{x - 2} \ \ x times (x - 2) = 6x - 15 \ \ {x}^{2} - 2x = 6x - 15 \ \ {x}^{2} - 8x + 15 = 0$

По теореме, обратной теореме Виета, получаем корни:

х1 = 3 и х2 = 5

Проверкой убеждаемся, что оба корни подходят.

ОТВЕТ: 3 ; 5

Answer 2

Ответ:   x₁ = 3;  x₂ = 5.

Решение:

Скажите, это ведь очень напоминает пропорцию, если к числу x приписать знаменатель 1? (Мне так кажется).

Воспользуемся правилом:

Произведение крайних членов пропорции равно произведению средних.

Получаем:

1 * (6x - 15) = x * (x - 2)

6x - 15 = x² - 2x

Теперь у нас есть обычное квадратное уравнение, которое нужно решить:

x² - 8x + 15 = 0.

Тут отлично сработает теорема Виета (дискриминантом решать как-то лень):

Сумма корней квадратного уравнения (ax² + bx + c = 0), при а = 1, равна третьему коэффициенту, а сумма - второму с противоположным знаком.

Тогда: 3 * 5 = 15,  3 + 5 = 8.

Проверим только ОДЗ:   x - 2 ≠ 0   ⇒   x ≠ 2. Все нормально.

Вот мы и получили ответ: x₁ = 3; x₂ = 5.