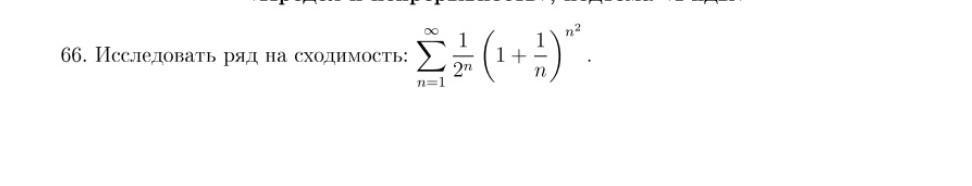Ответы
Ответ дал:
0
Ответ:
Ряд расходится.
Объяснение:
Исследовать ряд на сходимость:
- Используем признак Коши:
- Если для ряда
- u₁ + u₂ + u₃ +...+ uₙ + ... существует
,
- то этот ряд сходится при С < 1 и расходится при С > 1.
(второй замечательный предел)
С > 1 ⇒ ряд расходится
Ответ дал:
0
Ответ: ряд расходится.
Объяснение:
Применяем радикальный признак Коши - находим предел:
p<1 - ряд сходится;
р>1 - ряд расходится.
Ряд расходится.
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад